표본 (probabilistic sample, random sample, sample)
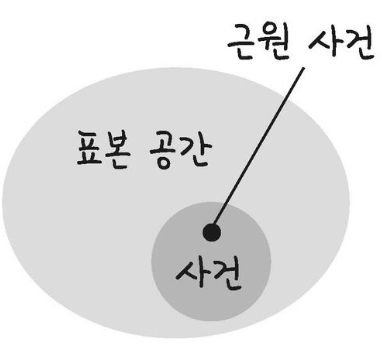
풀고자 하는 확률적 문제에서 발생할수 있는 하나의 현상 혹은 선택된 하나의 경우표본공간 (sample space) > Ω 표시
가능한 모든 표본의 집합
실험의 결과 하나하나를 모두 모은것
표본공간을 S 조사대상이 된 집단의 총합을 모집단 Ω로 표시
표본공간에서 임의의 집단을 사건(EVENT)
한 실험에서 나올 수 있는 모든 가능한 결과의 집합표본공간의 정의
어떤 표본(경우, 현상)이 가능하고 어떤 표본이 가능하지 않은가를 정의하는 작업
공리 (axiom)
수학에서 증명을 하지 않기로 약속한 명제
당연한것으로 가정을 하는 명제확률
사건(부분집합)을 입력하면 숫자(확률값)이 출력되는 함수
모든 사건에대하 확률은 실수, 0 또는 양수
표본공간(전체 집합)이라는 사건(부분집합)에 대한 확률은 1
표본공간에 모든 사건을 합친 것의 확률 = 표본공간의 모든 사건의 확률의 합
(1) 임의의 사건 A에 대해 확률 P(A)는 0 ≤ P(A) ≤1입니다.
(2) 반드시 일어나는 사건 S에 대해 확률 P(S) = 1입니다.
(3) 절대로 일어나지 않는 사건 ø에 대해 P(ø) = 0입니다.확률의 종류
이론적 확률 (수학적 확률)
- 누구라도 동일한 값으로 계산되는 엄밀한 확률
-> 수학적으로 정의됨
객관적 확률 (통계적 확률, 상대빈도 확률, 경험적 확률)
- 동일 조건/독립적으로 몇번 반복하였을 때의 발생 확률
-> 도수 이론(frequency theory)
- 반복된 실험에 기초한 `상대 빈도` 발생에 기반을 둠
- 대수의 법칙
주관적 확률 - 베이지안 관점
- 관찰자의 주관적 믿음/확신으로써 표현되는 확률
-> 주관적 견해(subjective view)
베이즈 확률
- 모집단을 미리 확정짓지 않고, 모수를 마치 확률변수 처럼 취급 대수의 법칙
시행이 많아질수록 통계적 확률은 수학적 확률에 가까워짐
확률적 데이터와 확률 변수
결정론적 데이터 (deterministic data)
생년월일처럼 한 번 물어보면 더이상 물어볼 필요가 없는 데이터
-> 변하지 않는 데이터
-> 항상 같은 값이 나오는 데이터
확률적 데이터 (random data, probabilistic data, stochastic data)
혈압, 체온처럼 환자가 내원할 때마다 물어보게 되는 데이터
-> 매번 변하는 데이터
-> 정확히 예측할 수 없는 값이 나오는 데이터
-> 부분의 데이터는 확률적 데이터
* 우리가 다루게 되는 대부분의 데이터는 확률적 데이터 *
분포 (distribution)
확률적 데이터에서 어떠한 값이 자주 나오고 어떠한 값이 드물게 나오는가를 나타내는 정보
범주형 데이터 -> (남,여)(학년) -> 카운트 플롯(count plot)
실수형 데이터 -> (실수형 숫자) -> 히스토그램(histogram)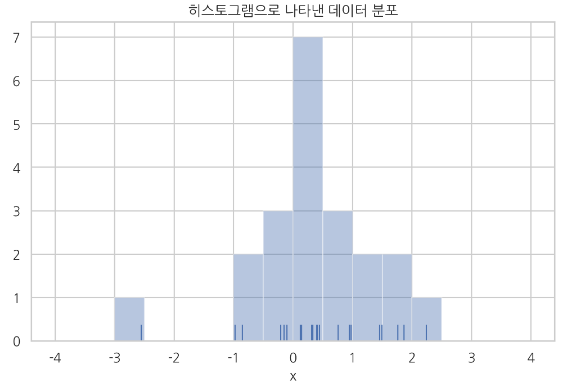
모집단 -> 표본공간 -> 확률변수 -> 실수 -> 확률분포 -> 확률 -> 확률의 검증, 테스트
확률 변수
확률공간의 표본을 입력으로 받아서 실수인 숫자로 바꾸어 출력하는 함수
실험 -> 동작 -> 동작을 통한 실수 값
동작을 확률 메커니즘
확률 변수는 확률 실험의 결과에 하나의 실수를 부여하는 함수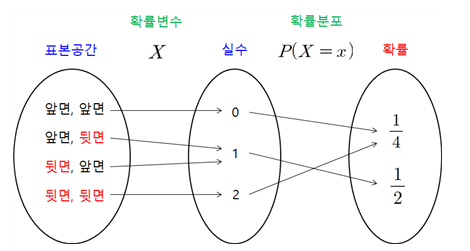
이산확률변수 (discrete random variable)
이산 : 연속적이지 않다 DRV
확률변수값이 연속적(continuous)이지 않고 떨어져(discrete) 있도록 정의할 수 있다면 -> 이산확률변수
표본공간의 원소의 개수가 무한대인 경우연속확률변수 (continuous random variable)
연속적이고 무한대의 실수 표본값을 가지는 확률변수를 연속확률변수
CRV
실수 -> 밀도의 합 ( 특정 구간의 합 -> 면적 ) -> 적분
촘촘히 이어져 있는 모든 구간의 합확률변수의 기댓값 -> 평균(mean)
이론적 평균을 확률변수의 기댓값(expectation)
이산확률변수의 기댓값은 표본공간의 원소 xi의 가중평균
가중치는 xi가 나올 수 있는 확률 즉 확률질량함수 p(xi)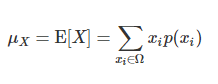
표본평균
일반적으로 부르는 평균(mean, average)의 정확한 명칭은 표본평균(sample mean, sample average)
모든 데이터의 합을 N 으로 나눈값
표본평균은 확률변수의 기댓값 근처의 값표본중앙값
전체 자료를 크기별로 정렬했을 때 가장 중앙에 위치하는 값
결측치 처리와 비슷함
평균 값과는 다르다
확률변수의 중앙값(median)은 중앙값보다 큰 값이 나올 확률과 작은 값이 나올 확률이 0.5로 같은 값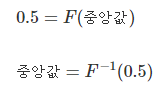
표본최빈값
데이터값 중 가장 빈번하게 나오는 값
연속확률분포의 최빈값(mode)은 확률밀도함수 p(x)의 값이 가장 큰 확률변수의 값
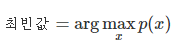
'데이터 수학 > 이론' 카테고리의 다른 글
| 확률분포 (probability distribution) (0) | 2023.02.22 |
|---|---|
| 선형 회귀 분석 (Linear Regression Analysis) (0) | 2023.02.20 |
| 엔트로피 (entropy) (0) | 2023.02.20 |
| 정밀도(Precision), 재현율(Recall), 정확도(Accuracy) (0) | 2023.02.20 |
| 벡터 (vector) (0) | 2023.02.17 |